Question:
An isosceles triangle has a base of 9.6 units long. If the congruent side lengths have measures to the first decimal place, what is the possible length of the sides? 9.7, 4.9, or 4.7
Answer:
4.9 is the shortest possible length of the sides.
Explanation:
Given:
The base of the triangle base = 9.2 units
To Find:
The shortest possible length of the sides = ?
Solution:
The Triangle Inequality Theorem states that the sum of any 2 sides of a triangle must be greater than the measure of the third side.
So According to the theorem
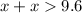
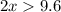
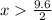

In the given option 4.9 is the shortest length greater than 4.8 that can be possible.