Answer:
The equation of hypotenuse is
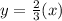 .
.
Explanation:
It is given that ΔABC and ΔA'B'C' are similar right triangles that share the same slope, m, on the coordinate plane.
ΔABC has base coordinates of A = (3, 2) and B = (6, 2).
Base of ΔABC = AB
Base of ΔA'B'C' = A'B'
ΔA'B'C' has a height coordinates of B' = (9, 2) and C' = (9, 6)
Height of ΔABC = BC
Height of ΔA'B'C' = B'C'
It means ∠B and ∠B' are right angles and points A, A', C, and C' lie on the hypotenuse.
If a line passes through two points
 and
and
 , then the equation of line is
, then the equation of line is
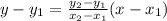
The hypotenuse passes through A(3,2) and C'(9,6) So, the equation of hypotenuse is
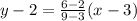

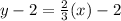
Add 2 on both sides.
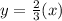
Therefore, the equation of hypotenuse is
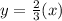 .
.