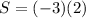Question

What is the sum of the infinite geometric series? Negative 3 minus three-halves minus three-fourths minus three-eighths minus three-sixteenths minus ellipsis

Answer 1

D. -6

Explanation:

on edge

Answer 2

`S=-6`

Explanation:

Sum Of A Geometric Series

Given a geometric series

`a_1,\ a_1.r,\ a_1.r^2,\ a_1.r^3,...`

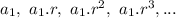
The sum of the infinite terms is given by

`\displaystyle S_n=(a_1)/(1-r)`

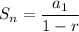
The sum converges only if

`|r|<1`

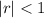
We are given the series as a sum:

`S=\displaystyle -3-(3)/(2)-(3)/(4)-(3)/(8)-(3)/(16)...`

Factoring by -3:

`\displaystyle -3\left (1+ (1)/(2)+(1)/(4)+(1)/(8)+(1)/(16)...\right )`

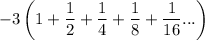
The expression in parentheses is a geometric series with

`a_1=1,\ r=1/2`

The sum can be computed by using the formula

`\displaystyle S_n=(1)/(1-1/2)`

`S_n=2`

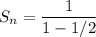
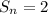
So our expression becomes

`S=(-3)(2)`

`\boxed{S=-6}`