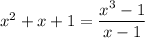
so we know
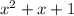 has roots equal to the cube roots of 1, not including
has roots equal to the cube roots of 1, not including
 itself, which are
itself, which are
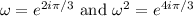
Any polynomial of the form
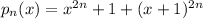 is divisible by
is divisible by
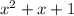 if both
if both
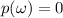 and
and
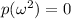 (this is the polynomial remainder theorem).
(this is the polynomial remainder theorem).
This means
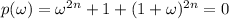
But since
 is a root to
is a root to
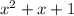 , it follows that
, it follows that
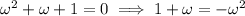
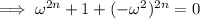
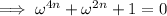
and since
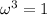 , we have
, we have
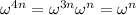 so that
so that

From here, notice that if
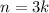 for some integer
for some integer
 , then
, then
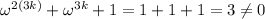
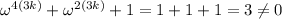
which is to say,
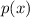 is divisible by
is divisible by
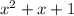 for all
for all
 in the given range that are *not* multiples of 3, i.e. the integers
in the given range that are *not* multiples of 3, i.e. the integers
 and
and
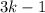 for
for
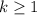 .
.
Since 2005 = 668*3 + 1, it follows that there are
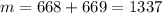 integers
integers
 such that
such that
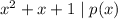 .
.
Finally,
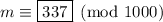 .
.