Question

A car accelerates uniformly from rest and

reaches a speed of 21.1 m/s in 14.1 s. The
diameter of a tire is 61.7 cm.
Find the number of revolutions the tire
makes during this motion, assuming no slipping.

Answer 1

Number of revolutions = 2.41

Step-by-step explanation:

According to first equation of motion:

`a=(v-u)/(t)`

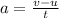
Here, a= acceleration

v = final velocity

u = initial velocity

According to question ,

a = ?

v = 21.1 m/s

t = 14.1 s

u = 0 (because object starts from rest)

`a=(v-u)/(t)`

`a=(21.1-0)/(14.1)`

`a=(21.1)/(14.1)`

`a=1.49m/s^(2)`

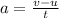
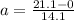
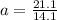
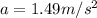
According to third equation of motion:

`2as=v^(2)-u^(2)`

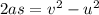
this can also be written as ,

`s=(v^(2)-u^(2))/(2a)`

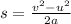
s = distance travelled by the object

a = 1.49

`s=(21.1^(2)-0^(2))/(2* 1.496)`

`s=(21.1^(2)-0^(2))/(2* 1.496)`

`s=(445.2-0)/(2.993)`

`s=(445.2)/(2.993)`

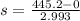
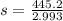
s = 148.79 m

Diameter of a tire = 61.7 cm

To calculate number of turns , divide distance by the diameter

`revolutions = (distance)/(diameter)`

`= (148.79)/(61.7)`

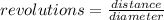
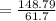
Number of revolutions = 2.41