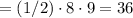Question

The base of the isosceles triangle is parallel to x-axis and has both end-points on the parabola y=x(10−x) and its vertex belongs to the x-axis. Find area of the triangle if the length of its base is 8.

Answer 1

36

Explanation:

We must determine the x and y intercepts of the parabola:

When y=0, x=0 or x=10

WE know that the point of the triangle base is x and x+8. We can substitute this into the parabola equation because the endpoints are on the parabola.

f(x+8)
`=-(x^2+16x+64)+10x+80`

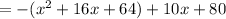
f(x+8)
`=-x^2-6x+16`

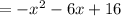
f(x)=f(x+8)

`-x^2+10x=-x^2-6x+16`

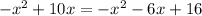
solve for x

`16x=16`

`x=1`

Therefore the heigh is f(1):

`=-1^2+10=9`

The area of the triangle is 1/2 base x height:

`=(1/2)\cdot{8}\cdot{9}=36`