Question

Five percent of workers in a city use public transportation to get to work. A transit authority offers discount rates to companes that have at least 30 employees who use public transportation to get to work. You randomly select 3 companies and ask their employees if they use public transportation below. Complete parts (a) through (c).

(a) Company A has 291 employees. What is the probability that Company A will get the discount.

(b) Company B has 540 employees. What is the probability that Company B will get the discount.

(c) Company C HAS 1013 employees. What is the probability that Company C will get the discount.

Answer 1

a) the probability that Company A will get the discount is 0

b) the probability that Company B will get the discount is 0.2753

c) the probability that Company C will get the discount is 0.9986

Explanation:

a) Let p(m) be the minimum proportion of workers needed at Company A who use public transportation to get to work in order the company can get discount offer by the transit authority.

Then
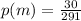`p(m)=(30)/(291)` ≈ 0.1031

The probability that Company A will get the discount can be stated as

P(z>z*) (p-value of z*) where z* is the z-score of 0.103 in the distribution of proportion of workers in the city who use public transportation to get to work.

z* can be calculated using the equation

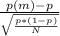`\frac{p(m)-p}{\sqrt{(p*(1-p))/(N) } }` where

• p(m) is the minimum proportion needed for company A get discount (0.1031)

• p is the proportion of workers in the city who use public transportation to get to work (0.05)

• N is the number of employees of Company A (291)

Then z*=
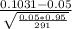`\frac{0.1031-0.05}{\sqrt{(0.05*0.95)/(291) } }` ≈ 4.15

P(z>4.15)=1-P(z<4.15)=1-1=0

b) for Company B:

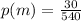`p(m)=(30)/(540)` ≈ 0.0556

z*=
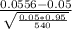`\frac{0.0556-0.05}{\sqrt{(0.05*0.95)/(540) } }` ≈ 0.597

P(z>0.597)=1-P(z<0.597)= 1-0.7247=0.2753

c) for Company C:

`p(m)=(30)/(1013)` ≈ 0.0296

z*=
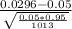`\frac{0.0296-0.05}{\sqrt{(0.05*0.95)/(1013) } }` ≈ -2.979

P(z>-2.979)=1-P(z<-2.979)=1-0.0014=0.9986