Answer:
Option B. 3.6
Explanation:
The given question is incomplete; here is the complete question.
If AB = 3, AD = 5, and DE = 6, what is the length of BC?
3.5
3.6
3.4
4
In the figure attached,
BC║ DE
Triangle ABC and ΔADE are the similar triangles [By AAA property of similar triangles]
By the property of similarity, corresponding sides of the similar triangles will be in the same ratio.
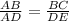
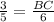
BC =
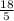
BC = 3.6
Therefore, Option B. 3.6 will be the answer.