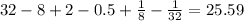Answer:
The sum of the first six terms is
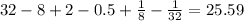
Explanation:
Given series is 32-8+2-0.5+...
We may write
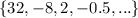
Let
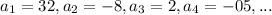
Common ratio
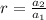

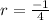
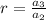
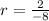
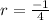
Therefore the common ratio is
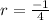
Therefore given sequence is of the form of Geometric sequence
The nth term of the geometric sequence is
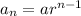
First to find the 5th and 6th term
That is substitute n=5 and n=6 ,a=32 and
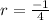 in above equation we get
in above equation we get
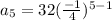
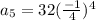
![a_(5)=32[((-1)/(4))* ((-1)/(4))* ((-1)/(4))* ((-1)/(4))]](https://img.qammunity.org/2021/formulas/mathematics/high-school/1dqifktw8nrm3g2uwkunb3e9zxzdgkh1wm.png)

Therefore
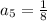
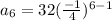
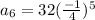
![a_(6)=32[((-1)/(4))* ((-1)/(4))* ((-1)/(4))* ((-1)/(4))* ((-1)/(4))]](https://img.qammunity.org/2021/formulas/mathematics/high-school/dpf9p0aqp96wg7a753cyid1lwhuxd09rxg.png)
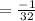
Therefore

Therefore the sum of the first six terms is

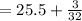
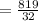
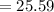
Therefore the sum of the first six terms is