Question

The points (7,13) and (-3,-11) are at the ends of a diameter. Find an equation for this circle.

Answer 1

`(x-2)^2+(y-1)^2=169`

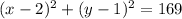
Explanation:

a general equation of a circle is:

`(x-a)^2+(y-b)^2=r^2`

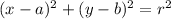
here,

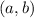`(a,b)`: is the coordinate of the center of the circle

`r`: is the radius

so these are the two things that we need to form our equation of the circle from the points (7,13) and (-3,-11)

since these are the ends of the diameter, the center of the circle would be the midpoint of the these two points!

so we'll calculate the midpoints using:

`(x_m,y_m) = \left((x_1+x_2)/(2),(y_1+y_2)/(2)\right)`

`(x_m,y_m) = \left((7-3)/(2),(13-11)/(2)\right)`

`(x_m,y_m) = (2,1)`

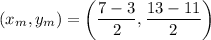
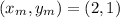
since this is also the coordinates of the center of the circle, we can also write them as:

`(a,b) = (2,1)`

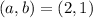
we have our values for 'a' and 'b'

Now to find the radius, all we need to do is to find the distance between the center and any of the endpoints of the diameter:

We'll use the distance formula, between the points (2,1) and (7,13)

`r = √((x_2-x_1)^2+(y_2-y_1)^2)`

`r = √((7-2)^2+(13-1)^2)`

`r = √((5)^2+(12)^2)`

`r = √(169)`

`r = 13`

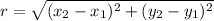
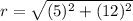
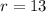
Now we have all the values: a,b,and r

we can plug them in the general equation of the circle:

`(x-a)^2+(y-b)^2=r^2`

`(x-2)^2+(y-1)^2=(13)^2`

`(x-2)^2+(y-1)^2=169`

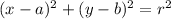
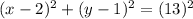
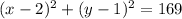
this is the equation of our circle