Question

Assume that women's heights are normally distributed with a mean of 63.6 inches and a standard deviation of 2.5 inches. If 150 women are randomly selected, find the probability that they have a mean height above 64.0

Answer 1

Answer: 0.0250

Explanation:

just took the test and missed it. Correct answer is 0.0250

Answer 2

0.9750

Explanation:

Given data: Normally distributed mean = 63.6 inches, standard deviation = 2.5 inches

Number of women, N = 150, Mean height = 64.0 inches

We know that
`Z=\frac{\bar{X}-\mu}{(\sigma)/(√(n))}`

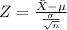
Now,
`P(\bar{X}>64)=P\left(\frac{\bar{X}-\mu}{(\sigma)/(√(n))}>(64.0-63.6)/((2.5)/(√(150)))\right)`

= P(Z > 1.959)

= P(Z > 1.96) (Rounding off the 1.959 we get 1.96)

In the normal table look row wise 1.9 and column wise 0.06,

We get the value 0.9750.

Hence,
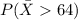`P(\bar{X}>64)` = 0.9750.