Question

I want to know which of two manufacturing methods will be better. I create 10 prototypes using the first process and 10 using the second. There were three defectives in the first batch and five in the second. What is a 95% confidence interval for the difference in the proportion of defectives?

Answer 1

Answer: (-0.620, 0.220)

Explanation:

The formula to find the confidence interval for the difference in true proportion of the two groups. is given by :-

`\hat{p}_1-\hat{p}_2\pm z^* \sqrt{\frac{\hat{p}_1(1-\hat{p}_1)}{n_1}+\frac{\hat{p}_2(1-\hat{p}_2)}{n_2}}`

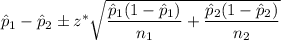
, where
`n_1` = Sample size for first group.

`n_2` = Sample size for second group.

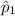`\hat{p}_1` = Sample proportion for first group.

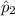`\hat{p}_2` = Sample proportion for second group.

z* = critical z-value.

Let first group be "group of prototypes by first process " and second group be "group of prototypes by second process".

`p_1` = Proportion of defectives in the first batch.

`p_2` = Proportion of defectives in the second batch.

From question , we have

`n_1=10` ,
`n_2=10` ,
`\hat{p}_1=(3)/(10)=0.3` ,
`\hat{p}_2=(5)/(10)=0.5`

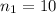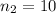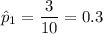By z-table , Critical value for 95% confidence interval is z* =1.96.

Substitute all values in formula , we get

`0.3-0.5\pm (1.96)\sqrt{(0.3(1-0.3))/(10)+(0.5(1-0.5))/(10)}`

`-0.2\pm (1.96)√(0.021+0.025)`

`-0.2\pm (1.96)√(0.046)`

`-0.2\pm (1.96)(0.21448)`

`-0.2\pm 0.4203808`

`=(-0.2-0.4203808,\ -0.2+0.4203808)\\\\=(-0.6203808,\ 0.2203808)\\\\\approx(-0.620,\ 0.220)`

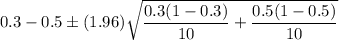
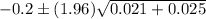
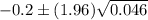
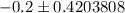
Hence, a 95% confidence interval for the difference in the proportion of defectives is (-0.620, 0.220).