Answer:
Null hypothesis:
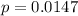
Alternative hypothesis:

A type of error II for this case would be FAIL to reject the null hypothesis that the population proportion is equal to 0.0147 when actually the alternative hypothesis is true (the true proportion is different from 0.0147).
Explanation:
Previous concepts
A hypothesis is defined as "a speculation or theory based on insufficient evidence that lends itself to further testing and experimentation. With further testing, a hypothesis can usually be proven true or false".
The null hypothesis is defined as "a hypothesis that says there is no statistical significance between the two variables in the hypothesis. It is the hypothesis that the researcher is trying to disprove".
The alternative hypothesis is "just the inverse, or opposite, of the null hypothesis. It is the hypothesis that researcher is trying to prove".
Type I error, also known as a “false positive” is the error of rejecting a null hypothesis when it is actually true. Can be interpreted as the error of no reject an alternative hypothesis when the results can be attributed not to the reality.
Type II error, also known as a "false negative" is the error of not rejecting a null hypothesis when the alternative hypothesis is the true. Can be interpreted as the error of failing to accept an alternative hypothesis when we don't have enough statistical power.
Solution to the problem
On this case we want to test if the proportion of children diagnosed with Autism Spectrum Disorder (ASD) is different from 0.0147, so the system of hypothesis would be:
Null hypothesis:
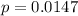
Alternative hypothesis:

A type of error II for this case would be FAIL to reject the null hypothesis that the population proportion is equal to 0.0147 when actually the alternative hypothesis is true (the true proportion is different from 0.0147).