Question

HELP PLEASE ASAP!!! Khan Academy unit test!

A circle with radius 3 has a sector with a central angle of 9/17 π radians .


What is the area of the sector?

Answer 1

The area of sector is 7.48 unit²

Explanation:

Given as :

The radius of circle = r = 3 unit

The measure of central angle =Ф =
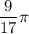`(9)/(17) \pi` radian

Let The area of sector = A unit²

Now, According to question

Area of sector = π× radius × radius ×
`(\Theta )/(360^(\circ))`

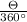
Or, A = π× r × r ×
`(\Theta )/(360^(\circ))`

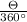
Or, A = π× r × r ×
`((9)/(17)\Pi  )/(360^(\circ))`

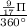
where π = 3.14

∵ 180° = π radian

So, 360° =
`(\Pi )/(180^(\circ))* 360^(\circ)` = 2 π radian

Or,, A = π× r × r ×
`((9)/(17\Pi ))/(2\Pi )`

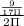
Or, A = π× r × r ×
`(9)/(34)`

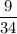
Or, A = 3.14 × 3 unit × 3 unit ×
`(9)/(34)`

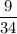
Or, A = 3.14 × 3 unit × 3 unit × 0.2647

∴ A = 7.48 unit²

So,The area of sector = A = 7.48 unit²

Hence, The area of sector is 7.48 unit² Answer