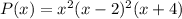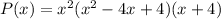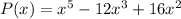Question

The polynomial of degree 5, P ( x ) has leading coefficient 1, has roots of multiplicity 2 at x = 2 and x = 0 , and a root of multiplicity 1 at x = − 4 Find a possible formula for P ( x ) .

Answer 1

`P(x)=x^5 - 12 x^3 + 16 x^2`

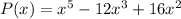
Explanation:

P ( x ) has leading coefficient 1

Root of multiplicity n at x= a can be written in factor form (x-a)^n

Roots of multiplicity 2 at x = 2

`(x-2)^2`

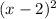
Roots of multiplicity 2 at x = 0

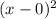`(x-0)^2` is
`x^2`

Roots of multiplicity 1 at x = -4

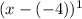`(x-(-4))^1` is
`x+4`

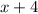
multiply all the factors

`P(x)= (x-2)^2 \cdot x^2 \cdot (x+4)`

`P(x)= x^2(x-2)^2 (x+4)`

`P(x)= x^2(x^2-4x+4) (x+4)`

`P(x)=x^5 - 12 x^3 + 16 x^2`