Question

As Potassium-40 decays, it becomes argon-40, as shown in the following graph.

Potassium-40 has a half-life of approximately 1.25 billion years. Approximately how many years will pass before a sample of potassium-40 contains one-fourth the original amount of parent isotope?
1.25 billion
2.5 billion
3.75 billion
5 billion

Answer 1

2.5 billion years

Step-by-step explanation:

Using the chart I provided you can see that when the potassium is at 1/4, it is on the "2". Since each mark stands for 1.25 billion, and 2 x 1.25 is 2.5, the answer is 2.5

Answer 2

The answer to your question is 2.5 billion years

Step-by-step explanation:

The initial amount of Potassium There is X

After 1,25 billion years There will be
`(X)/(2)`

After 1.25 billion years There will be
`(X)/(4)`

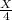
That means that the after 1.25 billion years + 125 billion years there will be one-fourth of the initial amount.

Total time = 2.5 billion years