Answer:
Option A is correct.
A) 64
Explanation:
Given:
The given expression =
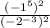
Now we need to simplify the given expression.
Solution:
=
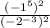
Rewrite the expression as.
=
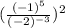 -------(1)
-------(1)
First we expand numerator
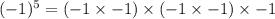
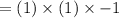
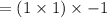
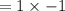
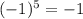
Similarly we simplify the denominator
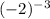 .
.
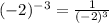
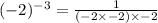
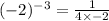
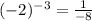
Now we substitute
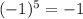 and
and
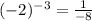 in equation 1.
in equation 1.
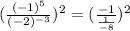
Negative sign is cancelled.
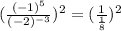
So we write the equation as.
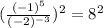
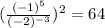
Therefore the answer is 64