Answer:
Option A) 0.0783
Explanation:
We are given the following information:
We treat delayed flight as a success.
P(Flight Delayed) = 15% = 0.15
Then the number of adults follows a geometric distribution, where
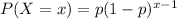
where x is the number of trails to get first success.
Now, we are given x = 5
We have to evaluate:

0.0783 is the probability that it will take 5 selections to find one flight that is delayed.
Option A) 0.0783