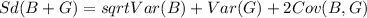Question

Question 1: 18% of high school boys and 10% of high school girls say they rarely or never wear seat belts. suppose one high school boy and one high school girl are selected at random, with the random variable of interest being the number in the pair who say they rarely or never wear seat belts. describe two ways of finding the expected value and standard deviation of this random variable, at least approximately.

Answer 1

See explanation below.

Explanation:

Notation

Let's define the following events:

B= A boy rarely or never wear seat belts

P(B) = 0.18

G= A girl rarely or never wear seat belts

P(G) =0.10

Solution to the problem

For this case we are interested on the following variable Y ="people who wear a seat belt" .And the possible values for Y are 0,1,2.

The expected value of a random variable X is the n-th moment about zero of a probability density function f(x) if X is continuous, or the weighted average for a discrete probability distribution, if X is discrete.

One way

Using the definition of random variable we can find the expected value like this:

`\mu = \sum_(i=1)^n Y_i P(Y_i)`

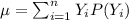
And the variance can be calculates like this:

`Var(Y) = \sigma^2 = E(Y^2) -[E(Y)]^2`

Where
`E(Y^2) = \sum_(i=1)^n Y^2_i P(Y_i)`

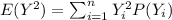
And then we can find the deviation like this:

`Sd(Y) = \sigma = √(E(Y^2) -[E(Y)]^2)`

Second way

Let B the random variable who represent if a boy rarely or never wear seat belts with possible values B=0,1 and G the random variable who represent if a girl rarely or never wear seat belts with possible values G=0,1. We can find the expected value like this:

`E(B+G) = E(B) +E(G)`

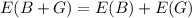
From definition of expected value.

And the variance like this:

Var(B+G) = Var(B) +Var(G) + 2Cov(B,G)[/tex]

If B and G are independent then
`Cov(B,G) = 0`

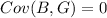
And the deviation is just this:

`Sd(B+G) = sqrt{Var(B) +Var(G) + 2Cov(B,G)}`