Question

A manufacturer knows that 14% of the products it produces are defective. Find the probability that among 7 randomly selected products, at least one of them is defective.

Answer 1

Answer: 0.6521

Explanation:

According to the Binomial distribution , the provability of getting x successes in n trials is given by :-

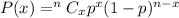`P(x)=^nC_xp^x(1-p)^(n-x)` , where p=probability of getting success in each trial.

Let x denotes the number of defective products.

here , n=7 and p =0.14

Then, the probability that among 7 randomly selected products, at least one of them is defective= P(X ≥ 1) =1- P(X<1)

= 1- P(X=0)

`=1-^7C_0(0.14)^0(1-0.14)^7`

`=1-(1(1)(0.86)^7\ \[\because ^nC_0=1]`

`=1-0.347927822217`

`=0.652072177783\approx0.6521`

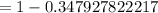
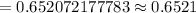
Hence, the probability that among 7 randomly selected products, at least one of them is defective is 0.6521 .