Answer:
a)
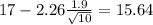
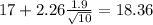
So on this case the 95% confidence interval would be given by (15.64;18.36)
b) 1. n=15, conf =95%
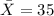 s=2.7
s=2.7
> round(qt(p=1-0.025,df=15-1),2)
[1] 2.14
> round(qt(p=0.025,df=15-1),2)
[1] -2.14
2. n=37, conf =99%
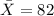 s=5.9
s=5.9
> round(qt(p=1-0.005,df=37-1),2)
[1] 2.72
> round(qt(p=0.005,df=37-1),2)
[1] -2.72
3. n=1009, conf =90%
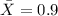 s=0.04
s=0.04
> round(qt(p=1-0.05,df=1009-1),2)
[1] 1.65
> round(qt(p=0.05,df=1009-1),2)
[1] -1.65
Explanation:
Part a: What is the lower bound to this confidence interval? 2 cm (round to 2 decimal places) What is the upper bound to this confidence interval? cm (round to 2 decimal places)
Previous concepts
A confidence interval is "a range of values that’s likely to include a population value with a certain degree of confidence. It is often expressed a % whereby a population means lies between an upper and lower interval".
The margin of error is the range of values below and above the sample statistic in a confidence interval.
Normal distribution, is a "probability distribution that is symmetric about the mean, showing that data near the mean are more frequent in occurrence than data far from the mean".
Solution to the problem
We have the following data:
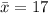 represent the sample mean
represent the sample mean
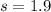 represent the sample deviation
represent the sample deviation
n =10 represent the sample size
The confidence interval for the mean is given by the following formula:
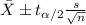 (1)
(1)
In order to calculate the critical value
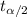 we need to find first the degrees of freedom, given by:
we need to find first the degrees of freedom, given by:
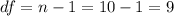
Since the Confidence is 0.95 or 95%, the value of
 and
and
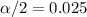 , and we can use excel, a calculator or a table to find the critical value. The excel command would be: "=-T.INV(0.025,9)".And we see that
, and we can use excel, a calculator or a table to find the critical value. The excel command would be: "=-T.INV(0.025,9)".And we see that
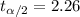
Now we have everything in order to replace into formula (1):
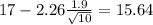
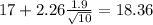
So on this case the 95% confidence interval would be given by (15.64;18.36)
Part b
1. n=15, conf =95%
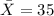 s=2.7
s=2.7
> round(qt(p=1-0.025,df=15-1),2)
[1] 2.14
> round(qt(p=0.025,df=15-1),2)
[1] -2.14
2. n=37, conf =99%
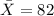 s=5.9
s=5.9
> round(qt(p=1-0.005,df=37-1),2)
[1] 2.72
> round(qt(p=0.005,df=37-1),2)
[1] -2.72
3. n=1009, conf =90%
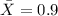 s=0.04
s=0.04
> round(qt(p=1-0.05,df=1009-1),2)
[1] 1.65
> round(qt(p=0.05,df=1009-1),2)
[1] -1.65