Question

the picture below shows the path that puppy Liz is running. The electrical post is 40 feet tall. Puppy liz usually starts at the bench post and runs until she gets to the fire hydrant, rest, and then she runs back to the bench. How far does puppy Liz run to get to the fire hydrant?

Answer 1

Puppy Liz has to run approx 70ft to get to fire hydrant from the bench post.

Explanation:

Let bench post be point A, fire hydrant be B and electrical post bottom be C and top be O.

We are given CO = 40ft

and angle BOC = 34°

angle AOC = 34 +23 = 57°

Let AB be y and AC be x

Clearly two right triangles are formed.

We can say,

In triangle BOC,

cos34° = Perpendicular ÷ Base = x÷40 => x = 40cos34°

and In triangle AOC

cos57° = Perpendicular ÷ Base = (x+y)÷40

substituting value of x from first equation to second we get,

40cos57° = 40cos34° + y

y = 40(cos57° - cos34°)

y = 40x1.75

y = 70ft which is the required answer.

Answer 2

The puppy runs 34 feet, approximately.

Explanation:

The problems models two triangles, the right triangle can be solved using trigonometric reasons and the other triangles can solved using law of cosines.

The distance that the puppy is running comprehend a side of the first triangle, however before finding that side, we need to first find the longest side, which is from the top of the electrical post to bench, which comprehend the hypothenuse of the bigger right triangle.

Applying trigonometric reasons, we have

`cos57=(40)/(x)\\ x=(40)/(cos57) \approx 73`

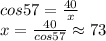
This is the longest hypothenuse.

`cos34=(40)/(y)\\ y=(40)/(cos34) \approx 48`

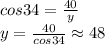
This is the common side, which goes from the top of the electric pole to the fire hydrant.

Now we know the common side between triangles and the longest hypothenuse, we use the law of cosines to find the side that comprehend the distance covered by the poppy

`d^(2)=x^(2)+y^(2)-2.x.y.cos23\\\\d^(2)=(73)^(2)+(48)^(2)-2(73)(48)cos23\\d=√(1182) \\d\approx 34`

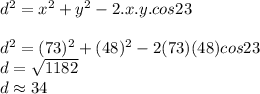
Therefore, the puppy runs 34 feet, approximately.