Question

Find an equation of the sphere with center (4, −12, 8) and radius 10.

Use an equation to describe its intersection with each of the coordinate planes. (If the sphere does not intersect with the plane, enter DNE.)

intersection with xy-plane
intersection with xz-plane
intersection with yz-plane

Answer 1

Explanation:

To find an equation of the sphere with center (4, −12, 8) and radius 10

`(x-4)^2+(y+12)^2+(z-8)^2 = 100`

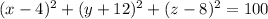
intersection with xy-plane

Put z=0

`(x-4)^2+(y+12)^2+(0-8)^2 = 100`

`(x-4)^2+(y+12)^2 = 36`

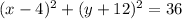
(A circle with centre at (4,-12) and radius 6)

intersection with xz-plane

Put y =0

`(x-4)^2+(0+12)^2+(z-8)^2 = 100`

`(x-4)^2+(z-8)^2 = -44`

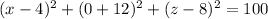
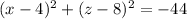
Sum of squares cannot be positive, so DNE

intersection with yz-plane

Put x=0

`(0-4)^2+(y+12)^2+(z-8)^2 = 100`

`(y+12)^2+(z-8)^2 = 84`

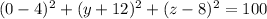
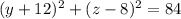
A circle in YZ plane with centre at y =-12 and z =8 and radius square root of 84