Answer:
The probability that a point chosen at random is in the blue region is 15/16.
Explanation:
In order to find the probability that a point chosen at random will lie in the blue region, we first have to find the area of the blue region.
The area
 of the large square is the product of its dimensions:
of the large square is the product of its dimensions:
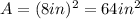
and for the smaller square area
 is:
is:
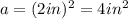
Therefore the area of the blue region is the area of the larger square minus the area of the smaller square.
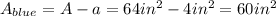
Therefore the probability that the point chosen at random is on the blue region is

The probability is
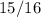 .
.