Question

A pitfall cited in Section 1.10 is expecting to improve the overall performance of a computer by improving only one aspect of the computer. Consider a computer running a program that requires 250 s, with 70 s spent executing FP instructions, 85 s executed L/S instructions and 40 s spent executing branch instructions

(5 min, sec 1.10)By how much is the total time reduced if the time for FP operations is reduced by 20%?


(5 min, sec 1.10) By how much is the time for INT operations reduced if the total time is reduced by 20%?
(5 min, sec 1.10) Can the total time be reduced by 20% by reducing only the time for branch instructions?

Answer 1

a) For this case the new time to run the FP operation would be reduced 20% so that means 100-20% =80% from the original time

`(1-0.2)*70 s =56s`

The reduction on this case is
`70-56 s=14s`

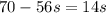
And since the new total time would be given by
`250-14=236 s`

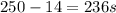
b) For this case the total time is reduced 20% so that means that the new total time would be (1-0.2)=0.8 times the original total time
`(1-0.2) *250s =200 s`

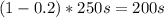
The original time for INT operations is calculated as:

`250 = 70+85+40 +t_(INT)`

`t_(INT)=55s`

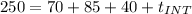
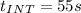
For this part the only time that was changed is assumed the INT operations so then:

`200 = 70+85+40 \Delta t_(INT)`

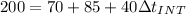
And then:
`\Delta t_(INT)= 200-70-85-40=5 s`

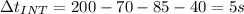
c) A reduction of the total time implies that the total time would be 205 s from the results above. And the time for FP is 70, for L/S is 85 and for INT operations is 55 s, so then if we add 70+85+55=210s, we see that 210>205 so then we cannot reduce the total time 20% just reducing the branch intructions.

Step-by-step explanation:

From the info given we know that a computer running a program that requires 250 s, with 70 s spent executing FP instructions, 85 s executed L/S instructions and 40 s spent executing branch instructions.

Part 1

For this case the new time to run the FP operation would be reduced 20% so that means 100-20% =80% from the original time

`(1-0.2)*70 s =56s`

The reduction on this case is
`70-56 s=14s`

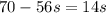
And since the new total time would be given by
`250-14=236 s`

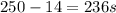
Part 2

For this case the total time is reduced 20% so that means that the new total time would be (1-0.2)=0.8 times the original total time
`(1-0.2) *250s =200 s`

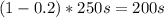
The original time for INT operations is calculated as:

`250 = 70+85+40 +t_(INT)`

`t_(INT)=55s`

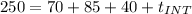
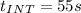
For this part the only time that was changed is assumed the INT operations so then:

`200 = 70+85+40 \Delta t_(INT)`

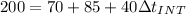
And then:
`\Delta t_(INT)= 200-70-85-40=5 s`

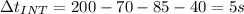
And we can quantify the decrease using the relative change:

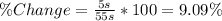`\% Change = (5s)/(55 s) *100 = 9.09\%` of reduction

Part 3

A reduction of the total time implies that the total time would be 205 s from the results above. And the time for FP is 70, for L/S is 85 and for INT operations is 55 s, so then if we add 70+85+55=210s, we see that 210>205 so then we cannot reduce the total time 20% just reducing the branch intructions.