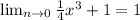Question

Let f be a function such that

Answer 1

B. The Limit is 1

Explanation:

Use the sandwhich theorem. The limit at both end as x approaches 0 is equal to 1, therefore f(x) must be equal to 1 as well because it's sandwhich between the two intervals.

Solving the Limits of the Endpoint:

`\lim_(n \to 0) (x^2-x^4)/(x^2)=(0)/(0)`

This is an in-determinant form so you must use L'Hopitals rule.

`\lim_(n \to 0) (x^2-x^4)/(x^2) \rightarrow \lim_(n \to 0) (2x-4x^3)/(2x) \rightarrow \lim_(n \to 0) (2-12x^2)/(2) =1`

`\lim_(n \to 0) {(1)/(4)x^3+1}=1`