Answer:
The measure of angle Y is 41.1°
Explanation:
Given as :
The figure is of triangle YES
The measure of angle S = ∠a = 70°
Let The measure of angle Y = ∠b = x°
The measure of side EY = a = 10 unit
The measure of side SE = b = 7 unit
Now, According o question
From The Law of Sin
 =
=
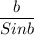 =
=
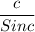
So, from figure
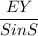 =
=
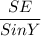
Compare with sin Law
 =
=
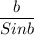
Or,
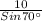 =
=
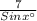
Or,
 =
=
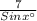
Or, 10.642 =
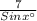
Or, Sin x° =
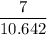
Or, Sin x° = 0.65777
∴ x =

i.e x = 41.1°
So,The measure of angle Y = x = 41.1°
Hence, The measure of angle Y is 41.1° Answer