Answer:
The velocity of the particle is 4.76 mm/s.
Step-by-step explanation:
Given that,
At x = 0, v = 16 mm/s
At x = 6 mm, v = 4 mm/s
The equation of acceleration is
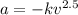
Here, k = constant
v= velocity
Th velocity of the particle along straight line

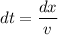 ....(I)
....(I)
The acceleration of the particle along a straight line
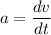
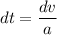 ....(II)
....(II)
From equation (I) and (II)
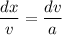
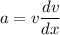
Put the value of a
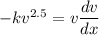
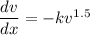
On integrating
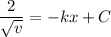 ....(III)
....(III)
Put the value of x = 0 and v = 16 mm/s in equation (III)


Now put the value of x = 6mm and v = 4 mm in the equation (III)
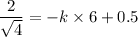
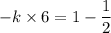
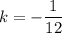
Put the value of k and C in equation (III)
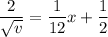
We need to calculate the velocity of the particle when x = 5
Put the value in the equation
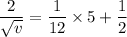
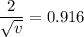
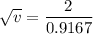
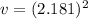
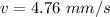
Hence, The velocity of the particle is 4.76 mm/s.