Question

The students' attitudes were measured by administering the Computer Anxiety Rating Scale (CARS). A random sample of 11 nursing students from Group 1 resulted in a mean score of 63.3 with a standard deviation of 3.7. A random sample of 13 nursing students from Group 2 resulted in a mean score of 70.2 with a standard deviation of 6.6. Can you conclude that the mean score for Group 1 is significantly lower than the mean score for Group 2? Let μ1 represent the mean score for Group 1 and μ2 represent the mean score for Group 2. Use a significance level of α=0.05 for the test. Assume that the population variances are equal and that the two populations are normally distributed.

Answer 1

There is enough evidence to claim that population mean 1 is less than population 2 at the 0.05 significance level.

Explanation:

We are given the following in the question:

Group 1:

`\mu_1 = 63.3\\\sigma_1 = 3.7\\n_1 = 11`

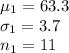
Group 2:

`\mu_2 = 70.2\\\sigma_2 = 6.6\\n_2 = 13`

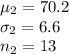
Alpha, α = 0.05

First, we design the null and the alternate hypothesis

`H_(0): \mu_1 \geq \mu_2\\H_A: \mu_1 < \mu_2`

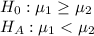
Since, the population variances are equal and that the two populations are normally distributed, we use t-test(pooled test) for difference of two means.

Formula:

Pooled standard deviation

`s_p = \sqrt{\displaystyle((n_1-1)\sigma_1^2 + (n_2-1)\sigma_2^2 )/(n_1 + n_2 - 2)}`

`t_(stat) = \displaystyle\frac{\mu_1-\mu_2}{s_p\sqrt{(1)/(n_1)+(1)/(n_2)}}`

`\text{Degree of freedom} = n_1 + n_2 - 2`

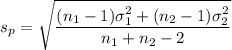
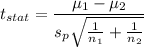
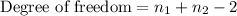
Putting all the values we get:

`s_p = \sqrt{\displaystyle((11-1)(3.7)^2 + (13-1)(6.6)^2 )/(11 + 13 - 2)} = √(29.9827) = 5.48`

`t_(stat) = \displaystyle\frac{63.3-70.2}{5.48\sqrt{(1)/(11)+(1)/(13)}} = -3.073`

`\text{Degree of freedom} = 11 + 13 - 2 = 22`

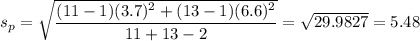
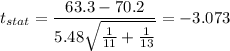
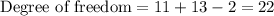
Now,

`t_(critical) \text{ at 0.05 level of significance, 22 degree of freedom } = -1.717`

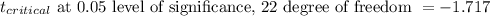
Since,

`t_(stat) < t_(critical)`

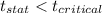
We fail to accept the null hypothesis and reject the null hypothesis. We accept the alternate hypothesis.

We conclude that the mean score for Group 1 is significantly lower than the mean score for Group 2.

There is enough evidence to claim that population mean 1 is less than population 2 at the 0.05 significance level.