Question

There is no prior information about the proportion of Americans who support the gun control in 2018. If we want to estimate 99% confidence interval for the true proportion of Americans who support the gun control in 2018 with a 0.36 margin of error, how many randomly selected Americans must be surveyed?

Answer 1

Answer: 13

Explanation:

If the prior population proportion is unavailable then the formula to find the sample size is given by :-

`n=0.25((z^*)/(E))^2`

, where z* = Critical z-value

E = margin of error

Let p be the proportion of Americans who support the gun control in 2018.

As per given , we have

Confidence level = 99%

The critical z-value for 99% confidence interval is 2.576 ( BY z-table)

Margin of error : E= 0.36

Since there no prior information about the proportion of Americans who support the gun control in 2018.

So , the required sample size to estimate 99% confidence interval would be:

`n=0.25((2.576)/(0.36))^2=0.25(7.16)^2`

`n=0.25(51.2656)=12.8164\approx13`

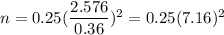
Hence, 13 Americans should be surveyed.