Answer:
The roots of the quadratic equation are.
t = -0.78
t = -4.62
Explanation:
Assume: we find the roots of the given quadratic equation.
Given:
the given expression is.
T squared plus 5.4t plus 3.6 equals 0
Rewrite the equation as.
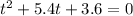
Now, we first find the root of the above equation.
Use quadratic formula with
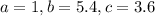 .
.
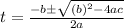
Put a, b and c value in above equation.
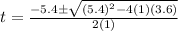
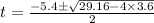
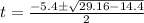
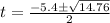
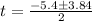
For positive sign
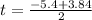
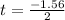
t = -0.78
For negative sign
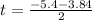
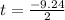
t = -4.62
Therefore the roots of the quadratic equation t = -0.78 or t = -4.62
.