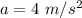The position of a particle moving in a straight line at any time t is x(t) = 2t^2 + 6t + 5. What is the acceleration of the particle at t=3

Question

asked Mar 14, 2021 178k views

1 Answer

Glog · Answer 1 · 2021-03-18T21:24:53+0000

Answer:

The acceleration of the particle at any time t

$a = 4\ m/s^(2)$

Explanation:

Given:

The position of a particle moving in a straight line at any time t is.

x(t) = 2t^(2) + 6t + 5

The velocity of the particle

v = (d)/(d(t))(2t^(2) + 6t + 5)

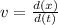
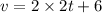
v= 2* 2t + 6

v= 4t + 6

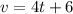
So the velocity of the particle
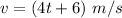
$v= (4t + 6)\ m/s$

The acceleration of the particle

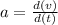
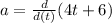
a = (d)/(d(t))(4t + 6)

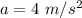
$a = 4\ m/s^(2)$

In this condition the acceleration does not depending upon the time, so the acceleration is constant

Therefore the acceleration of the particle at any time t
$a = 4\ m/s^(2)$