Question

Dr. Christina Cuttleman, a nutritionist, claims that the average number of calories in a serving of popcorn is 75 with a standard deviation of 7. A sample of 50 servings of popcorn yields an average of 78 calories. Check Dr. Cuttleman's claim at a = 0.05.

Answer 1

`z=(78-75)/((7)/(√(50)))=3.03`

`p_v =2*P(Z>3.03)=0.002446`

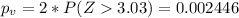
If we compare the p value and the significance level given
`\alpha=0.05` we see that
`p_v<\alpha` so we can conclude that we have enough evidence to reject the null hypothesis, so we can conclude that the true mean is significantly different from 75.

Step-by-step explanation:

Previous concepts and data given

The margin of error is the range of values below and above the sample statistic in a confidence interval.

Normal distribution, is a "probability distribution that is symmetric about the mean, showing that data near the mean are more frequent in occurrence than data far from the mean".

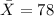`\bar X=78` represent the sample mean

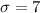`\sigma=7` represent the assumed population standard deviation

n=50 represent the sample selected

`\alpha=0.05` significance level

State the null and alternative hypotheses.

We need to conduct a hypothesis in order to check if the mean is actually 75, the system of hypothesis would be:

Null hypothesis:
`\mu = 75`

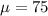
Alternative hypothesis:
`\mu \\eq 75`

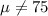
If we analyze the size for the sample is > 30 and we know the population deviation we can apply a z test to compare the actual mean to the reference value, and the statistic is given by:

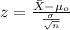`z=(\bar X-\mu_o)/((\sigma)/(√(n)))` (1)

z-test: "Is used to compare group means. Is one of the most common tests and is used to determine if the mean is (higher, less or not equal) to an specified value".

Calculate the statistic

We can replace in formula (1) the info given like this:

`z=(78-75)/((7)/(√(50)))=3.03`

P-value

Since is a two sided test the p value would be:

`p_v =2*P(Z>3.03)=0.002446`

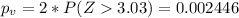
Conclusion

If we compare the p value and the significance level given
`\alpha=0.05` we see that
`p_v<\alpha` so we can conclude that we have enough evidence to reject the null hypothesis, so we can conclude that the true mean is significantly different from 75.