Question

A man on the deck of a ship is 14 ft above water level. He observes that the angle of elevation of the top of a cliff is 40 degrees and the angle of depression of the base is 20 degrees. Find the distance of the cliff from the ship and the height of the cliff if the base of the cliff is at sea level.

Answer 1

The distance of the ship from the cliff is 38.465 feet

The height of the cliff is 46.28 feet.

Explanation:

As shown in the figure attached
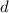`d` is the distance from the ship to the cliff, and
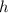`h` is the height of the cliff from the ship.

From trigonometry

`tan(20^o)=(14)/(d)`

`d=(14)/(tan(20^o))=38.465\:feet.\\\\\boxed{d=38.465ft}`

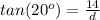
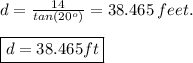
This is the distance to the cliff.

And we have

`tan(40^o)=(h)/(d)`

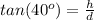
since
`d=38.465ft`

`h=d*tan(40^o)=38.465*tan(40^o)=32.28ft`

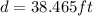
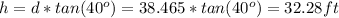
Ad the height of the cliff is just
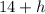`14+h` or

`32.28+14=46.28 ft\\\\\boxed{height=46.28ft}`

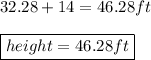
Which is the height of the cliff.