Question

Which shows all the critical points for the inequality x2-4/x2-5x+6<0

Answer 1

the answer is b

Explanation:

Answer 2

x = ±2, 3 are the critical points of the given inequality.

Explanation:

The given inequality is
`((x^(2)- 4))/(x^(2)-5x+6)<0`

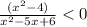
To find the critical points we will equate the numerator and denominator of the inequality to zero.

For numerator,

`x^(2)-4=0`

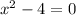
(x - 2)(x + 2) = 0

x = ±2

For denominator,

x² - 5x + 6 = 0

x² - 3x -2x + 6 = 0

x(x - 3) -2(x - 3) = 0

(x - 3)(x - 2) = 0

x = 2, 3

Therefore, critical points of the inequality are x = ±2, 3 where the sign of the inequality will change.