Answer:
B) Debra's snowball will stay in the air longer than Mary's snowball.
Correct. For Debra we have a time to get up let's say
 and the same time to find the reference level and from the reference level to hit the ground let's say that takes
and the same time to find the reference level and from the reference level to hit the ground let's say that takes
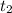 so the total time to hit the ground for Debre is
so the total time to hit the ground for Debre is
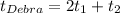
For Mary the object not need time to get up so then just take let's assume
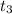
But we know that
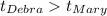
D) Debra's snowball has exactly the same acceleration as Mary's snowball.
True. For this case we assume that the only force acting is the grviaty and the resistence of the air can be neglected. So then the acceleration for both are the same.
Step-by-step explanation:
Assuming the following options:
A) Both snowballs will take the same amount of time to hit the ground.
False. As we can see on the figure attached, for Debra we have a time to get up let's say
 and the same time to find the reference level and from the reference level to hit the ground let's say that takes
and the same time to find the reference level and from the reference level to hit the ground let's say that takes
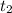 so the total time to hit the ground for Debre is
so the total time to hit the ground for Debre is
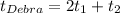
For Mary the object not need time to get up so then just take let's assume
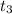
But we know that
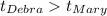
B) Debra's snowball will stay in the air longer than Mary's snowball.
Correct. For Debra we have a time to get up let's say
 and the same time to find the reference level and from the reference level to hit the ground let's say that takes
and the same time to find the reference level and from the reference level to hit the ground let's say that takes
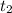 so the total time to hit the ground for Debre is
so the total time to hit the ground for Debre is
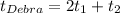
For Mary the object not need time to get up so then just take let's assume
But we know that
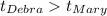
C) Mary's snowball will stay in the air longer than Debra's snowball.
False that's totally opposed from the result that we obtain,
D) Debra's snowball has exactly the same acceleration as Mary's snowball.
True. For this case we assume that the only force acting is the grviaty and the resistence of the air can be neglected. So then the acceleration for both are the same.
E) Mary's snowball has a greater downward acceleration than Debra's snowball.
False, as we can see before the same acceleration is acting for both snowballs.