Question

Business A c Charges $50 for a service call, plus an additional $36 per hour for labor. Business a charge is $35 for a service call,Plus an additional $39per hour for labor. Let x represent the number of Hours of labor and Y represent the total charge. Write a system of equations you could solve to find the length of a service call for which both businesses charge the same amount.

Answer 1

The system of equation to find the length of service call is
`\left \{ {{y=50 +36x} \atop {y =35 +39x}} \right.`.

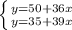The length of service call for which both businesses charge the same amount is 5 hours.

Explanation:

Given:

Let the 'x' represents number of hours of labor.

Also Let the 'y' represent the Total charge.

For Business A:

Fixed charge = $50

Charge of labor for each hour = $36

Amount of total charge is the sum of fixed charge and charge of labor for each hour multiplied number of hours of labor

framing in equation form, we get;

`y=50 +36x \ \ \ \ equation \ 1`

For Business B:

Fixed charge = $35

Charge of labor for each hour = $39

Amount of total charge is the sum of fixed charge and charge of labor for each hour multiplied number of hours of labor

framing in equation form, we get;

`y =35 +39x \ \ \ \ equation \ 2`

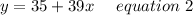
Hence The system of equation to find the length of service call is
`\left \{ {{y=50 +36x} \atop {y =35 +39x}} \right.`.

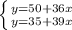Now to find the length of service call for which both businesses charge the same amount, we will make both the equation equal we get;

`50+36x=35+39x`

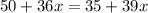
Now we solve the equation,

Combining the like terms, we get;

`50-35=39x-36x\\\\15=3x`

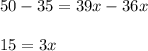
Dividing both side by '3' using division property, we get;

`(15)/(3)=(3x)/(3)\\\\5=x`

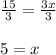
Hence The length of service call for which both businesses charge the same amount is 5 hours.