Answer:
A minimum of 4 bits will be needed.
Step-by-step explanation:
As there are 12 months in a year so will need 12 need combinations.
Number of bits can be determined by the powers of 2. By this we mean:
 Two unique combinations can be made that are 0 and 1.
Two unique combinations can be made that are 0 and 1.
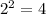 4 unique combinations can be made.
4 unique combinations can be made.
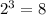 8 unique combinations can be made.
8 unique combinations can be made.
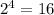 16 unique combinations can be made.
16 unique combinations can be made.
Now we will have to use 4 bits so that 12 unique combinations may be assigned to each month.
Following is given the bit pattern for each month:
JANUARY => 0000
FEBRUARY => 0001
MARCH => 0010
APRIL => 0011
MAY => 0100
JUNE => 0101
JULY => 0111
AUGUST => 0110
SEPTEMBER => 1000
OCTOBER => 1001
NOVEMBER => 1010
DECEMBER => 1011
i HOPE IT WILL HELP YOU!