Question

What is the area of rhombus ABCD? Enter your answer in the box. Do not round at any steps. put the answer in units²

Answer 1

Therefore the Area of Rhombus ABCD is 36 unit².

Explanation:

Given:

ABCD is a Rhombus

A = (-1,0)

B = (5,-3)

C = (-1,-6)

D = (-7 ,-3)

To Find:

Area of Rhombus ABCD = ?

Solution:

We know that Area of Rhombus is given as

`\textrm{Area of Rhombus}=(1)/(2)* d_(1)* d_(2)`

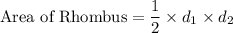
Where ,

d₁ and d₂ are the Diagonals.

We have,

Diagonals as AC and BD,

Using Distance Formula we get

`l(AC) = \sqrt{((x_(2)-x_(1))^(2)+(y_(2)-y_(1))^(2) )}`

Substituting coordinates A and C we get

`l(AC) = \sqrt{((-1-(-1))^(2)+(-6-0)^(2) )}=√(36)\\l(AC)=6\ unit`

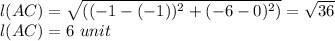
Similarly for BD we have,

`l(BD) = \sqrt{((5-(-7))^(2)+(-3-(-3))^(2) )}=√(144)\\l(BD)=12\ unit`

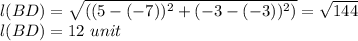
Now Substituting AC and BD in Formula we get

`\textrm{Area of Rhombus}=(1)/(2)* AC* BD`

`\textrm{Area of Rhombus}=(1)/(2)* 6* 12=36\ unit^(2)`

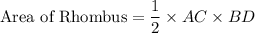
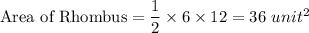
Therefore the Area of Rhombus ABCD is 36 unit².