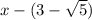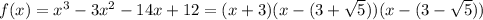Answer:
The zeros are x+3 ,
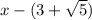 and
and
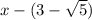
and is given by
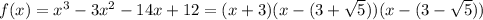
Explanation:
Given polynomial function is
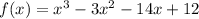
To find the zeros:
Equate the polynomial function to zero
That is f(x)=0
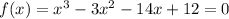
By using synthetic division method we can find zeros
-3_| 1 -3 -14 12
0 -3 18 -12
_______________
1 -6 4 0
Therefore x+3 is a zero
Ie., x=-3
Now the quadratic equation is
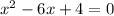
Here a=1 , b=-6 and c=4
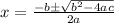
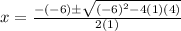
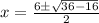
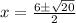
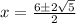
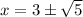
Therefore
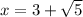 and
and
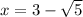
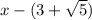 and
and
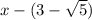
Therefore the zeros are x+3 ,
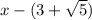 and
and