Question

If triangle TLY is similar to triangle CHK, find LY

The sides from T to L is 25 from L to Y is 4x-1.
On the other triangle Side, C to H is 10 and from H to K is x+5

Answer 1

Therefore the Length LY is 35 unit.

Explanation:

Given:

ΔTLY is Similar to ΔCHK

TL = 25

LY = 4x -1

CH = 10

HK = x + 5

To Find:

LY = ?

Solution:

Δ TLY ~ Δ CHK ........Given

If two triangles are similar then their sides are in proportion.

`(TL)/(CH) =(LY)/(HK) \textrm{corresponding sides of similar triangles are in proportion}\\`

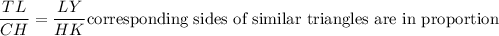
Substituting the values we get

`(25)/(10) =(4x-1)/(x+5)\\\\(5)/(2) =(4x-1)/(x+5)\\\\5(x+5)=2(4x-1)\\5x+25=8x-2\\3x=27\\\\x=(27)/(3)=9\\\\x=9`

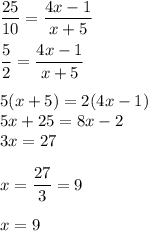
Substituting 'x' in LY we get

`LY=4* 9 - 1=36-1=35\ unit`

Therefore the Length LY is 35 unit.