Question

The graph of the function C(x) = −0.34x2 + 12x + 62 is shown. The function models the production cost, C, in thousands of dollars for a tire company to manufacture a tire, where x is the number of tires produced, in thousands:

graph of a parabola opening down passing through points negative 4 and 57 hundredths comma zero, zero comma 62, 1 and 12 hundredths comma 75, 17 and 65 hundredths comma 167 and 55 hundredths, 34 and 18 hundredths comma 75, and 39 and 87 hundredths comma zero

If the company wants to keep its production costs under $75,000, then which constraint is reasonable for the model?

−4.57 ≤ x ≤ 39.87
1.12 ≤ x ≤ 34.18
−4.57 ≤ x ≤ 1.12 and 34.18 ≤ x ≤ 39.87
0 ≤ x < 1.12 and 34.18 < x ≤ 39.87

Answer 1

D is the answer

Explanation:

took the test

Answer 2

0 ≤ x < 1.12 and 34.18 < x ≤ 39.87

Explanation:

Let

x ----> is the number of tires produced, in thousands

C(x) ---> the production cost, in thousands of dollars

we have

`C(x)=-0.34x^(2) +12x+62`

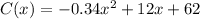
This is a vertical parabola open downward (the leading coefficient is negative)

The vertex represent a maximum

The graph in the attached figure

we know that

Looking at the graph

For the interval [0,1.12) ----->
`0\leq x<1.12`

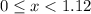
The value of C(x) ---->
`C(x) < 75`

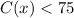
That means ----> The production cost is under $75,000

For the interval (34.18,39.87] ----->
`34.18 < x\leq 39.87`

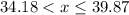
The value of C(x) ---->
`C(x) < 75`

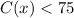
That means ----> The production cost is under $75,000

Remember that the variable x (number of tires) cannot be a negative number

therefore

If the company wants to keep its production costs under $75,000 a reasonable domain for the constraint x is

0 ≤ x < 1.12 and 34.18 < x ≤ 39.87