Question

Riley and Erik have earned a total of 135 tokens to buy items in the school store. The ratio of the number of tokens that Riley had to the number of tokens that Erik has is 8 to 7. How many tokens does Riley have?

Answer 1

Riley has 72 tokens

Explanation:

System of Equations

We have two conditions for the tokens Riley and Erik have earned. Let's call x and y to the number of tokens of Riley and Erik respectively. The first condition states that

`x+y=135`

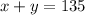
Solving for y

`y=135-x`

The second condition is that the ratio of the number of tokens that Riley had to the number of tokens that Erik has is 8 to 7. It's written as

`\displaystyle (x)/(y)=(8)/(7)`

Or equivalently

`7x=8y`

Replacing y from the first equation

`7x=8(135-x)`

Operating

`7x=1080-8x`

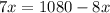
Simplifying

`15x=1080`

`\boxed{x=72}`

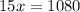
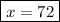
Riley has 72 tokens