Answer:
Therefore , the faster route distance is 13 miles.
Explanation:
Given:
AB = 5 miles to East
BC = 12 miles to South
To Find:
AC = Faster and Direct Route = ?
Solution:
Consider ΔABC as a Right Angle Triangle, hence By Pythagoras Theorem,

Substituting the values we get
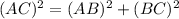
Therefore , the faster route distance is 13 miles.