Answer:
(-6,-8),(7,18) and (-4,6),(2,3) lie on perpendicular lines
Explanation:
we know that
The formula to calculate the slope between two points is equal to
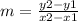
step 1
Find the slope of the pair (-6,-8),(7,18)
substitute
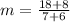
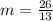
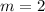
step 2
Find the slope of the pair (6,4),(4,12)
substitute
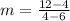
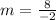
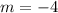
step 3
Find the slope of the pair (-4,6),(2,3)
substitute
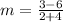
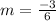
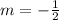
step 4
Remember that
If two lines are perpendicular, then their slopes are opposite reciprocal (the product of their slopes is equal to -1)
In this problem
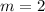 and
and
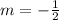 are opposite reciprocal
are opposite reciprocal
therefore
(-6,-8),(7,18) and (-4,6),(2,3) lie on perpendicular lines