Answer:
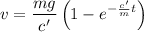
The option marked iv. is the correct answer
Explanation:
Ordinary Differential Equation (ODE)
The problem is an application of the Ordinary Differential Equations in physics. We are given the functions for the two forces acting on an object. We apply the second Newton's law to find the dynamics conditions as follows

Knowing that the acceleration is the derivative of the velocity, thus

We know
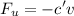
and also
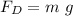
Replacing in the first equation:
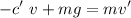
Rearranging
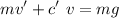
![\displaystyle v'+(c')/(m)\ v=g\ \ \ \ \ .....[eq\ 1]](https://img.qammunity.org/2021/formulas/mathematics/middle-school/2ra5w4dugxzcx4bq2b556xuo0omsberd9d.png)
This is a linear non-homogeneous ordinary differential equation. We'll solve it by finding the homogeneous solution first which takes the form
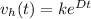
It takes us to solve the characteristic equation:
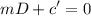
Solving for D
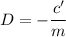
The homogeneous solution is
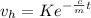
The particular solution depends on the form of the independent term located in the right side of the equation. In this case, it's a constant, thus the particular solution has the form
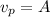
Where A is a constant we must find, by replacing it in the original differential equation. We compute

Replacing in (Eq 1):
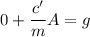
We find the value of A
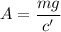
The complete solution for v is
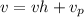
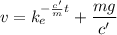
We have the initial condition

That gives us the value of k
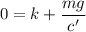
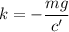
Thus, the solution for v is
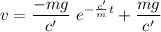
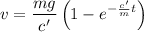
The option marked iv. is the correct answer