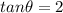Question

find the angle of projection at which the horizontal range is twice the maximum height of a projectile​

Answer 1

`\theta= 63.43^o`

Step-by-step explanation:

Projectile Motion

If an object is launched in free air forming an angle with the horizontal, it describes a special motion path called parabola. The horizontal speed is constant throughout the movement, while the vertical speed goes from its initial value going down to zero in the highest point of the trajectory, and finally increases back to the same speed it was launched with but in opposite direction.

The horizontal distance traveled by the object in any time t is

`\displaystyle x=v_o\ cos\theta\ t`

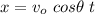
The vertical distance is given by

`\displaystyle y=v_o\ sin\theta t-(g\ t^2)/(2)`

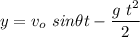
To find the time taken by the object to reach the maximum height, we set y=0, find the time and then divide the flight time by 2:

`\displaystyle y=0`

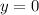
Solving for t

`\displaystyle t=(2v_osin\theta)/(g)`

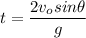
Replacing t in the horizontal distance, gives us the range or maximum distance

`\displaystyle x_m=v_o\ cos\ \theta ((2\ v_o\ sin\theta)/(g))`

`\displaystyle x_m=(2v_o^2\ cos\theta.sin\theta)/(g)`

`\displaystyle x_m=(2v_o^2\ sin\theta.cos\theta)/(g)`

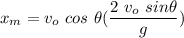
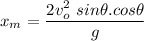
Using half the time of the total time, we get the maximum height

`\displaystyle y_m=(v_o^2\ sin^2\theta)/(2g)`

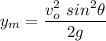
Since

`\displaystyle x_m=2y_m`

`\displaystyle (2\ v_0^2\ sin\theta \ cos\theta)/(g)=(2\ v_o^2\ sin^2\theta)/(2g)`

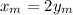
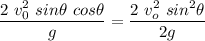
Simplifying and solving for \theta

`\displaystyle tan\theta =2`

`\boxed{\theta= 63.43^o}`