Question

Sales

The cumulative sales S (in thousands of units) of a new product after it has been on the market for t years are modeled by S = 50(1 - ekt).
During the first year, 8000 units were sold.
(a) Solve for k in the model.
(b) What is the saturation point for this product?
(c) How many units will be sold after 5 years?
(d) Use a graphing utility to graph the sales function.

Answer 1

a). k = -0.1743

b).
`\lim_(t \to \infty)S=50` is be the saturation point.

c). 29000 units will be sold.

Explanation:

The cumulative sales of a new product after t years is modeled by

S =
`50(1-e^(kt))`

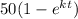
a). During first year number of units sold were 8000.

That means for t = 1 and S = 8 (Since S is in thousands of units),

8 =
`50(1-e^(k))`

`1-e^(k)=(8)/(50)`

`1-e^(k)=0.16`

`e^(k)=0.84`

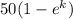
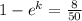
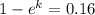
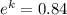
By taking natural log on both the sides

`ln(e^(k))=ln(0.84)`

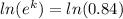
k = -0.1743

b). To get the saturation point,

`\lim_(t \to \infty)S= \lim_(t \to \infty)50(1-e^(kt))`

`\lim_(t \to \infty)S= \lim_(t \to \infty)50(1-(1)/(e^(0.1743t)))`

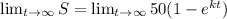
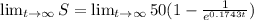
Since
`\lim_(t \to \infty)(1)/(e^(0.1743t))=0`

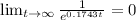
Therefore,
`\lim_(t \to \infty)S=50` will be the saturation point.

c). For t = 5, we have to find the number of units sold.

S =
`50(1-e^(-0.1743* 5))`

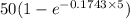
= 50(1 - 0.4813)

= 29000 units will be sold after 5 years.