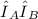Answer:
(a) Yes,
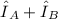
(b) Yes,
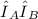
Explanation:
First, lets understand what are eigenvectors and eigenvalues?
Note: I am using the notation
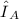 to denote Lambda(A) sign.
to denote Lambda(A) sign.
 is an eigenvector of matrix A with eigenvalue
is an eigenvector of matrix A with eigenvalue
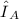
 is also eigenvector of matrix B with eigenvalue
is also eigenvector of matrix B with eigenvalue
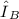
So we can write this in equation form as
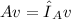
So what does this equation say?
When you multiply any vector by A they do change their direction. any vector that is in the same direction as of
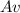 , then this
, then this
 is called the eigenvector of
is called the eigenvector of
 .
.
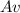 is
is
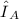 times the original
times the original
 . The number
. The number
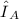 is the eigenvalue of A.
is the eigenvalue of A.
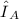 this number is very important and tells us what is happening when we multiply
this number is very important and tells us what is happening when we multiply
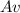 . Is it shrinking or expanding or reversed or something else?
. Is it shrinking or expanding or reversed or something else?
It tells us everything we need to know!
Bonus:
By the way you can find out the eigenvalue of
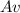 by using the following equation:
by using the following equation:
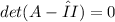
where I is identity matrix of the size of same as A.
Now lets come to the solution!
(a) Show that
 is an eigenvector of
is an eigenvector of
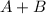 and find its associated eigenvalue.
and find its associated eigenvalue.
The eigenvalues of
 and
and
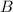 are
are
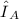 and
and
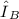 , then
, then
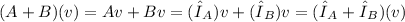
so,
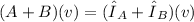
which means that
 is also an eigenvector of
is also an eigenvector of
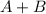 and the associated eigenvalues are
and the associated eigenvalues are
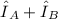
(b) Show that
 is an eigenvector of
is an eigenvector of
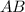 and find its associated eigenvalue.
and find its associated eigenvalue.
The eigenvalues of
 and
and
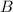 are
are
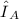 and
and
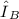 , then
, then
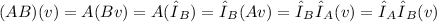
so,
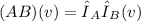
which means that
 is also an eigenvector of
is also an eigenvector of
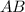 and the associated eigenvalues are
and the associated eigenvalues are