Question

Radioactive Waste The rate at which radioactive waste is entering the atmosphere at time t is decreasing and is given by Pe^-kt, where P is the initial rate. Use the improper integral

∫^[infinity]_0 Pe^-kt dt
with P = 50 to find the total amount of the waste that will enter the atmosphere for each value of k.
k=0.04

Answer 1

`\displaystyle{\int^(\infty)_0 {50e^(-0.04t)}\, dt}=1250`

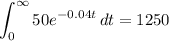
Explanation:

Given:

`T =\displaystyle{\int^(\infty)_0 {Pe^(-kt)} \, dt}`

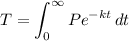
where,

T = total amount of waste

P = 50, the initial rate

k = 0.04

t = time

`T =\displaystyle{\int^(\infty)_0 {50e^(-0.04t)} \, dt}`

now we need to solve this integral!

`T =\displaystyle{50\int^(\infty)_0 {e^(-0.04t)} \, dt}`

`T = \left|50\left((e^(-0.04t))/(-0.04)\right)\right|^(\infty)_0`

`T = \left|-1250e^(-0.04t)\right|^(\infty)_0`

`T = (-1250e^(-0.04(\infty)))-(-1250e^(-0.04(0)))`

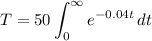
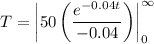
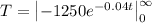
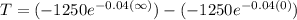
when any number has a power of negative infinity it is 0. because:
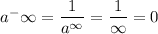`a^-{\infty} = (1)/(a^(\infty)) = (1)/(\infty) = 0`, like something being divided by a very large number!

`T = (-1250(0))-(-1250e^0)`

`T = 1250`

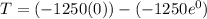
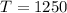
this is the total amount of waste